Reibung & Haftreibung
Folie 3: Haftreibung
Diese Folie bringt Ergänzungen zu den Begriffen „Haftreibung“ und „Reibungskraft“ über das hinaus, was zu diesen Themen in den üblichen Physikbüchern zu finden ist. Das Anspruchsniveau ist an die Sekundarstufe I angepasst. Die linke Hälfte der Folie beschäftigt sich mit besonderen Eigenschaften des Materials Gummi. Die hier angesprochenen Eigenschaften von Gummi haben dazu geführt, dass es als ideales Material für die Konstruktion von Fahrzeugreifen erkannt wurde und konkurrenzlos benutzt wird.
Eigenschaften von Gummi
Links oben:
Gummi ist ein Material, das zugleich die Eigenschaften einer elastischen Feder wie die einer rein viskosen Flüssigkeit aufweist. Um die letztgenannte Eigenschaft zu verdeutlichen, muss folgendes Modell betrachtet werden: Die Flüssigkeit ist in einem Zylinder eingeschlossen, durch den man einen Kolben schieben kann. In dem Kolben befinden sich Überströmkanäle, damit man den Kolben überhaupt durch die Flüssigkeit bewegen kann. Eine solche Vorrichtung ist im Bild links dargestellt; die elastischen Eigenschaften des Gummis werden rechts durch die rot eingezeichnete Feder repräsentiert. [Gummi kann ferner – je nach herrschender Temperatur und Abfolgehäufigkeit (Stoßfrequenz), mit der belastende Stöße auf das Material erfolgen – auch noch das Verhalten eines starren glasartigen Körpers annehmen.]
Mitte links:
Die Eigenschaften von Gummi sind im Diagramm Kraft bzw. Federwege entsprechend farbig markiert. Hier wird das Verhalten, das ein ideal elastischer Körper in Folge einer bestimmten Kraftwirkung zeigt, dem eines ideal viskosen Körpers gegenübergestellt. Da in der Sekundarstufe I die Begriffe „Frequenz“ und „Schwingung“ noch nicht hinreichend bekannt sein dürften, wurde als Kraftverlauf ein einfaches lineares Anwachsen der Kraft bis zu einem Maximalwert und ein sofortiger Rückgang auf Null angenommen. Dieser Kraftverlauf in Abhängigkeit von der Zeit t wird in grün (ohne Maßstab) wiedergegeben.
Visko-Elastische Eigenschaften
Wenn nun der Körper ausschließlich elastische Eigenschaften hätte, wie die im oberen Bild rot dargestellte Feder, so würde er dem „Hookeschen Gesetz“ folgen und einen Federweg (Auslenkung s) zeigen, wie er in der rot gestrichelten Diagrammlinie im mittleren Bild Kraft bzw. Federwege (ebenfalls ohne Maßstab) dargestellt ist. Eine Auslenkung (s) würde sofort mit dem Beginn der Kraftwirkung einsetzen, nach dem „Hookeschen Gesetz“ linear mit der Kraft zunehmen, und mit Ende der Kraftwirkung augenblicklich zurückgehen – von einem evtl. Nachfedern abgesehen. Hätte andererseits der Körper ausschließlich viskose Eigenschaften, so würde er allein mit dem im oberen Bild gelb eingetragenen Modell des ölgefüllten Kolbens (also ohne die rote Feder!) korrekt dargestellt. Hierbei würde eine Formänderung erst mit einer gewissen zeitlichen Verzögerung nach dem Beginn der Kraftwirkung einsetzen.
Dieser Zeitverzug wird in der Fachliteratur mit „Hysterese“ bezeichnet. Hört die Kraftwirkung auf, so bleibt die eingetretene Verformung erhalten und geht nicht zurück. Dieses Verhalten gibt die gelb gestrichelte Diagrammlinie im mittleren Bild wieder. Natürlich verhält sich ein realer Autoreifen in dieser Hinsicht anders, denn Gummi besitzt beide Eigenschaften. Daher sorgt die rückstellende Kraft des „elastischen Anteils“ dafür, dass die Verformung durch eine umgekehrte Kraftwirkung wieder rückgängig gemacht wird. Die tatsächlichen Kraftwirkungen auf einen Reifen ähneln außerdem Schwingungen mit verschiedenen Frequenzen, verursacht durch grobe (Makro-)Rauigkeit der Straße (siehe Foto Mitte links) und feine (Mikro-) Rauigkeit des Straßenbelags.
Auch Resonanzen im Fahrzeug selbst (Motor, Karosserie, Auspuff) und Rolleffekte tragen zu einer Fülle gleichzeitig auf die Reifen wirkender Schwingungen bei. Die Kraftwirkungen sind dabei nicht nur, wie man zunächst vermuten könnte, ausschließlich nach oben orientiert, sondern durchaus auch als Zugkräfte nach unten (!). Der Grund liegt in molekularen Wechselwirkungen im Kontaktbereich Reifen/Straße (van-der-Waals-Kräften), wodurch auch rückstellende Kraftwirkungen nach unten hervorgerufen werden können. Eine überzeugende Begründung in der Sekundarstufe I für die Existenz solcher Kräfte kann man liefern, indem man mit den Schülern als Freihandexperiment Versuche mit völlig ebenen Glasscheibchen ausführt (wenn vorhanden, alte Dia-Deckgläschen, ansonsten Präparat-Glasscheiben aus dem Biologieunterricht).
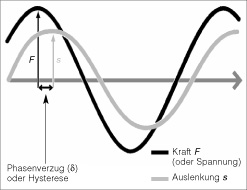
Die Abbildung zeigt das Verformungsverhalten eines gemischt visko-elastischen Materials in Abhängigkeit von einer sich sinusförmig ändernden Kraft.
Unten links:
Das Diagramm bezieht sich auf eine andere Eigenschaft von Gummi, die Auswirkungen auf die Haftung hat. Es geht um die veränderliche sogenannte „Steifigkeit“ des Materials. Damit ist nicht einfach eine gewisse Härte gemeint, die ein Mensch vielleicht durch Befühlen beurteilen könnte, sondern eher der „Widerstand des Materials“, den Kraftstößen zu folgen, die mit verschiedenen Frequenzen einwirken. Die hier gemeinte Materialeigenschaft „Steifigkeit“ ist daher sowohl von der Temperatur als auch von der Frequenz der Stoßabfolge abhängig. Auf Sek-I-Niveau reduziert kann man sagen: Einerseits gilt: Wenn die Umgebungstemperatur T zurückgeht, nehmen die elastischen Eigenschaften des Gummis ab und die „Steifigkeit“ nimmt zu. Im Diagramm „Gummi-Steifigkeit“ auf der Folie unten links zeigt dies die rote Kurve: Bei niedrigen Temperaturen verhält sich das Material glasartig hart, bei höheren Temperaturen ist die „Steifigkeit“ gering und das Material ist gummi-elastisch. Die Übergangstemperatur zwischen Glas- und Gummiverhalten wird kurz mit „Glastemperatur Tg„ bezeichnet. Da nur ein grundsätzlicher Effekt dargestellt werden soll, wurde auf den Temperaturmaßstab verzichtet. Die absolute Höhe der „Glastemperatur“ hängt auch von der Frequenz der anregenden Kraftstöße ab. So läge sie beispielsweise bei einer Stoßfrequenz von 10 Hertz (Rollunwuchten, u. Ä.) bei -20 °C und bei einer Frequenz von 100 kHz (Mikrorauigkeit der Straße) bei +10 °C. Andererseits nimmt diese „Steifigkeit“ bei einer angenommenen festen Umgebungstemperatur zu, wenn die Stoßfrequenz f zunimmt (blaue Kurve). Die Haftung des Reifens ist im Übergangsbereich rund um die „Glastemperatur“ am höchsten, wo sich das Gummi also weder extrem „glasartig hart“ noch „gummiartig weich“ verhält, im sogenannten optimalen Haftungsbereich. Aufgabe der Konstrukteure eines Reifens ist also, im Hinblick auf den geplanten Einsatz des Reifens (Sommer-/Winterreifen; Temperaturen am Einsatzort; Stoßarten und -frequenzen auf dem erwarteten Untergrund) die Gummimischung so auszulegen, dass der angedeutete optimale Haftungsbereich im Alltagseinsatz des Reifens eingehalten werden kann.
Haftung
Auf der rechten Hälfte der Folie finden sich grundlegende Informationen zum Thema Haftung. Die Gegenüberstellung oben rechts erläutert die Bedeutung bzw. Definition der Haftreibungszahl µ. Sie zeigt, wie wichtig es für den µ-Wert ist, die beiden beteiligten Materialien anzugeben und dass der Wert je nach Materialien ganz unterschiedlich ist. Um Missverständnisse auszuschließen sei noch kurz erwähnt, dass es sich bei den angegebenen Horizontalkräften jeweils um Haftkräfte handelt, die unmittelbar vor dem Eintritt des Gleitens als Maximalwerte an den Kraftmessern messbar werden. Erwähnt sei auch, dass unter idealen Bedingungen auf trockener Straße Haftzahlen über 1 auftreten können. Dies sieht man z. B. bei Motorradfahrern, die sich in Kurven über 45 Grad zur Seite neigen können, ohne wegzurutschen.
Der Tangens des maximal möglichen Seitenneigungswinkel entspricht mathematisch dem Verhältnis von FHaft zu FG , also genau der Definition der Haftreibungszahl m. Kann sich der Fahrer mehr als 45 Grad zur Seite neigen (tan 45 ° = 1), folgt daraus, dass der µ-Wert größer als 1 sein muss. Leider sind konkrete Aufgaben hierzu in der Sekundarstufe I noch nicht möglich, da die Winkelfunktionen zu dem Zeitpunkt, an dem das Thema Haftreibung im Physikunterricht in der Regel zu erwarten ist, noch nicht zur Verfügung stehen dürften. Die Abbildung unten rechts zeigt die erhebliche Verringerung des maximalen µ-Wertes der Haftung beim Auftreten von „Aquaplaning“. Dabei kann die Wasserhöhe einige mm bis 0,5 mm betragen. Die Tabelle unten verdeutlicht, dass die Haftung mit zunehmender Wasserhöhe und mit zunehmender Geschwindigkeit dramatisch abnimmt.
Kopiervorlage
Mit Kopiervorlage 3 wird eine in den üblichen Physikbüchern nicht dargestellte Möglichkeit aufgezeigt, durch einen einfachen Schülerversuch die Haftreibungszahl zu ermitteln. (Mit demselben Versuchsaufbau lässt sich natürlich auch der Wert der Gleitreibungszahl ermitteln. Dann muss die Größe h für den Fall festgehalten werden, dass der Körper auf der Unterlage abwärts gleitet.)
Will man den Schülern:innen die im Grunde leichte Aufgabe stellen, µ zu ermitteln, ergibt sich das Problem: Zu Hause besitzt niemand einen Kraftmesser! Außerdem entfällt die Möglichkeit, mithilfe der vielleicht vorhandenen Küchenwaage die Gewichtskraft zu bestimmen und auf diesem Umweg an die Hangabtriebskraft bzw. die Normalkraft zu kommen, da zu dem Zeitpunkt der Behandlung des Themas „Reibung“ im Fach Physik die Trigonometrie noch nicht zur Verfügung stehen dürfte, auch wäre der Winkel schwierig zu messen.
Das vorgeschlagene Verfahren benutzt daher reine Längenmessungen, von denen die Bestimmung der Länge l sogar extrem einfach ist. Was hierbei dann aus der Mathematik zur Herleitung der Formel benutzt wird, dürfte evtl. schon zu diesem Zeitpunkt zur Verfügung stehen. Man benutzt zum einen den Satz, dass in „ähnlichen Dreiecken“ die entsprechenden Seiten ein gleiches Verhältnis bilden (evtl. setzt man dies nicht als bekanntes Mathematikwissen voraus, sondern begründet per Anschauung). Zum anderen benutzt man den Satz von Pythagoras. Beide Hilfsansätze werden auf der Kopiervorlage genannt. Die damit mögliche mathematische Herleitung der Formel richtet sich an gute Mathematiker im Klassenverband; ansonsten kann eine Hilfe durch den Lehrer erforderlich werden. (Der Versuch selbst lässt sich natürlich auch ohne mathematische Herleitung der Formel durchführen).
Die praktische Ausführung des Versuchs kann sowohl als Hausaufgabe gestellt wie auch in der Schule erledigt werden. (Wenn vom Lehrer entsprechend variantenreiches Material beschafft wird, verspricht auch die letztgenannte Möglichkeit einiges!) Für die Ausführung zu Hause kann der erwartete Umfang vom Lehrer präzisiert werden; die Aufgabentexte auf der Kopiervorlage können übernommen werden oder als Anregung dienen. Weitere selbst erstellte Rechen- und Diskussionsaufgaben von ähnlicher Art wie in den gängigen Physiklehrbüchern, die hier die zusätzliche Chance nutzen, die auf der Folie gegebenen Informationen zur Verringerung der Haftreibung bei Aquaplaning einzusetzen, werden dem Lehrer empfohlen!
LERNZIELE: Die Schüler:innen sollen
- die auf der Folie vorgestellten besonderen Eigenschaften des Werkstoffes Gummi mit eigenen Worten beschreiben können
- eine präzisere Vorstellung von der Haftreibung (Haftreibungszahl) bekommen, insbesondere durch eigene Ausführung der Versuche von der Kopiervorlage
- den Unterschied von Haft- und Gleitreibung beschreiben können
- die Entstehung von und Gefahren durch „Aquaplaning“ erläutern können